7. Results
7.1 Average treatment effects
Table 4 shows the estimated average effects of establishing a low emission zone on monthly average PM10 concentrations (part a) and the number of days in exceedance of the 24h limit per month (part b).In column (1a), only station, month and year fixed effects were used to control for unobserved effects. As can be seen, the treatment with a basic LEZ leads to a reduction of 0.902µg/m³ in the average monthly concentrations, so almost 1µg/m³ per year. This treatment effect is significant at the 5% level, while the establishment of an air quality plan or an advanced LEZ do not yield significant results. This effect even increases slightly when the number of inhabitants in each year at city level is added as a control variable in column (2a). However , when introducing interacted state-month fixed effects in column (3a) to control for region-specific developments, such as economic developments or weather conditions, the treatment effect is reduced to almost half its absolute size and turns insignificant. The same pattern can be observed for the treatment with an advanced LEZ. While in column (1a) and (2a) a rather large treatment effect of -1.4µg/m³ can be observed, the coefficient turns insignificant in column (3a) when controlling for region-specific effects. Hence , it seems like the state-month fixed effects capture some unoberserved underlying variables or events relevant to both treatment assignment and outcome. The effects in columns (1a) and (2a) are thus likely to suffer from an omitted variable bias. From these results, it can be concluded that it is not possible to establish a causal effect from the introduction of an AQP, a basic or an advanced low emission zone on PM10 average concentrations. For the advanced low emission zones, the relatively small sample size of 14 observations and the short observation period (all but one city introduced an LEZ in the beginning of 2010) should be kept in mind. When more data becomes available, the results should therefore be checked again.
Examining part b) of table 4, where the number of days in violation of the 24 hour limit value per month is used as a dependent variable, a more robust treatment effect can be found for the introduction of a basic low emission zone. Even when controlling for region-specific developments in column (3b), an average reduction of 0.436 days in violation of the 24h limit per month is achieved, translating into a reduction of approximately 5 days per year. The introduction of the stricter standards of an advanced LEZ does not lead to significant additional improvements in comparison to the basic LEZ, but one should keep in mind again the small number of observations treated with an advanced LEZ.
Table 4: Estimates of average treatment effects /…/ [Table omitted]
7.2 Heterogeneous treatment effects
The treatment effects of air quality plans and low emission zones in section 7.1 were established as average treatment effects, assuming that the policy exerts the same effect on all treated units, regardless of different characteristics they might exhibit. However , it is possible that the introduction of an LEZ affects PM10 concentrations differently depending on city characteristics. To test for such heterogeneity, observed characteristics can be interacted with the treatment indicators. To see this, consider the following simplified reformulation of model (1):
(2) ![]()
αi as the treatment effect is now allowed to vary between units or groups. Assuming that αi depends linearly on observable characteristics, this can be expressed as follows13:
![]()
Where the error term is supposed to have a conditional expected value of zero, ![]() . Replacing αi in model (2) by the linear combination yields:
. Replacing αi in model (2) by the linear combination yields:
(3) ![]()
The heterogeneity is captured by the interaction term (ziτit)’ and estimated by ρ. For example, the treatment effect could depend on the initial level of pollution. An example for such a specification is given below, where Ihigh represents observations with high initial pollution levels. The coefficients α1 – α6 should then capture possible heterogeneous effects of treatment with an air quality plan (AQP), a basic low emission zone (LEZ 1) or an advanced low emission zone (LEZ 2)
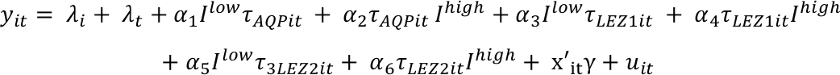
Heterogeneous treatment effects with respect to city sizes
To establish heterogeneous treatment effects with respect to the city size, an indicator variable was created, classifying the city where a monitoring station is placed either as “small” (up to 100,000 inhabitants), “medium” (100,000 to 500,000 inhabitants), or “large” (more than 500,000 inhabitants). The distribution of treated and control stations within these groups can be found in table A3 in the appendix. These indicator variables were then interacted with the treatment variables to capture possible heterogeneous effects. The model specifications used correspond to columns (2) and (3) in table 4. It has to be noted that heterogeneity can only be established for the treatment with a basic LEZ, since all cities that have an advanced LEZ in place fall in the category of large cities.
Table 5 shows the results for the heterogeneous effects. Column (1a) suggests a reduction of approximately 1.2µg/m³ in average concentrations following the introduction of a basic LEZ in large cities, but once again this effect turns insignificant when fixed effects capturing region-specific developments are introduced in column (1b). When turning to the limit violations of the 24h limit in part b) of table 5, a more robust treatment effect for large cities can be found. In both specifications used, the coefficient for the basic LEZ in large cities is significant, while no treatment effect is found for small and medium cities. For cities with more than 500,000 inhabitants, a reduction of ca 8 days with an average concentration of more than 50µg/m³ per year is found. This effect is considerably larger than the average effect found in table 4, indicating that it is the large cities that also drive the average treatment effect.
Table 5: Heterogeneous effects: City size [Table not shown]
Heterogeneous treatment effects with respect to initial PM10 pollution levels
Another interesting aspect regarding the introduction of LEZs is to analyze if treatment effects vary with respect to the initial levels of PM10 pollution and non-compliances with the limit values. Therefore , the sample was divided into two groups, representing cities with high and low initial average monthly concentrations in the years 2004–2007. This time span was selected to guarantee that the concentrations were not influenced by the introduction of the low emission zone yet. Average monthly concentrations of the 42 treated cities spread between 22.3 and 47.4 µg/m³. The cutoff value for being a highly polluted city was chosen at 31µg/m³, dividing the sample into a group of 22 observations below this value and a group of 20 above the cutoff. A dummy variable interacted with the treatment variable was then used to identify possible heterogeneous effects. For the number of days in exceedance of the 24 hour limit, a cutoff value with respect to the initial average number of limit violations was created. The average number of non-compliances in the years 2004 to 2007 for the treated observations varied between 14.8 and 134 days per year. A cutoff value of 35 days per year was selected, dividing the treated units in two equally large groups of 21 observations each. Due to the small sample size of cities treated with an advanced low emission zone and also a low degree of variation within this group, the analysis is limited to the treatment with a basic low emission zone. The results are displayed in table 6 below.
For the monthly average concentrations, the results of previous specifications are confirmed. For highly polluted cities, there seems to be a treatment effect when not controlling for region-specific effects, but this effect disappears when introducing state-month dummies. All other coefficients are insignificant in both specifications.
For the second dependent variable, the number of days in exceedance of the 24 hour limit, the results in part b) of table 6 show again some heterogeneity in the treatment effect for the basic LEZ. The effect is only found to be significant for cities experiencing frequent violations of the limit; and it is again larger than the average treatment effect, amounting to a reduction of almost 9 non-compliance days per year. This is interesting, since the cutoff value for violating the limit frequently was chosen at the politically defined maximum value of 35 days per year14. However , it should be kept in mind that the cutoff value of 35 days per year was chosen as an average over the period 2004–2007. That means that the group of cities in “frequent” violation has basically been in non-compliance with this limit value every year between 2004 and 2007, while cities that recorded single years in violation are most likely to be placed in the “few” group. Therefore , it cannot be concluded from table 9 that each city that once has been in violation of the standard should introduce a LEZ because it reduces the exceedance days, but the results show that the policy only works for cities that are more or less constantly in non-compliance with the law. For such cities, introducing a LEZ could actually be a way to get closer to compliance with EU law.
Table 6: Heterogeneous effects: Initial PM10 concentrations 2004–2007 [Table not shown]
7.3 Spillover effects
Although low emission zones are spatially clearly defined, the introduction of the policy might affect the pollution situation even in nearby locations, as was explained in section 3. The presence of spillover effects is interesting per se, but could also be a problem for the identification of treatment effects. If the introduction of an LEZ leads to a decrease in PM10 concentrations at surrounding measuring points that are included as control observations, the identified treatment effect would be too small. If, on the other hand, an LEZ leads to an increase of concentrations at such stations, the treatment effect would be overestimated. To identify such spillover effects, the data on violations of the 24 hour limit is analyzed once again.
To get a first idea about the presence and sign of spillover effects, all control units that are located in a state where at least one station is treated are excluded from the sample, assuming that these are the units where spillover effects might be present. This reduces the control group significantly: Of the 80 original control units, 39 were excluded, resulting in a treatment group of 42 observations versus a control group of 41 stations. This change in the control group has to be kept in mind when comparing the results in table 7 to previous. Moreover , the distance between some of the excluded stations and an LEZ can still be quite big, even if they are located in the same state. For such stations, spillover effects are quite unlikely. This model can therefore only serve as a rough test if the treatment effects might be biased due to spillover effects.
As can be seen in table 7, the treatment effect gets larger in both specifications when compared to the basic results in table 4b, especially when it is controlled for region-specific time effects. The treatment effect in column (2) would translate into approximately 8.5 fewer days with concentrations above 50µg/m³ per year, but as explained, the results are not directly comparable. However , they indicate that positive spillover effects could be present, causing the average results in table 4 being too small in absolute size.
Table 7: Effects on violations of the 24h limit excluding control observations in states where a LEZ is implemented [Table not shown]
To check more formally for spillover effects, a variable that indicates a “secondary treatment” for the control stations within states that also host LEZs was created. This secondary treatment was defined to start at the same time as the treatment of the closest treated station. Then, the same regressions as in the basic models including the secondary treatment variable were run. However , no significant secondary treatment effect could be found for the observations located in the same states as treated cities. As this could be due to the fact that some of the observations classified as “secondary treated” are actually located quite far away from treated cities, in a second and third step, only observations within 50km respectively 25km of a treated city were classified as secondary treated. Though the coefficient of the secondary treatment got larger when moving closer to the originally treated observations, no result was significantly different from zero. In a final attempt , only those observations that were actually located in an LEZ city, but outside the LEZ itself, were classified as secondary treated, resulting in eight secondary treated observations
As can be seen in table 8, no significant treatment effect can be established for the stations within the same city. Therefore , it seems like LEZs have an effect only in the designated region and do not significantly improve the pollution situation in adjacent areas. However , the analysis done above also indicates that the policy does not affect adjacent observations negatively, for example by creating additional traffic flows outside the LEZ. Moreover , it should be recognized that the estimate of the regular treatment effect of the basic low emission zone translates into approximately six days above the 24h limit less per year, compared to five in the original level in table 4. This suggests that the presence of non-treated station within LEZ cities might lead to a small underestimation of the treatment effect in absolute size in the original specification.
Table 8: Testing for spillover effects on non–treated observations within the same city [Table not shown]
7.4 Sensitivity Analysis
Although the results seem consistent and in line with expectations in all model specifications used so far, this section will conduct a sensitivity analysis of the results, in order to preclude threats to validity arising from omitted control variables and the inclusion of some cities with more than one measuring station in the sample.In a first check, it will be examined if the estimation results are robust to adding additional variables that could be correlated with both treatment status and the outcome. As explained previously, economic developments at a local level could provide one source for such omitted variables. To test for this, additional data on local employment rates and disposable income per capita was collected, following Greenstone (2004) and Auffhammer et al. (2010). Data was available at either the city level or the corresponding municipality level from the German Federal Statistics Agency until 2009 on a yearly basis. Thus , the following estimation results exclude all observations for 2010. All the model specifications from table 4a and b are replicated; the new control variables are added in columns (3) and (5).
The results in table 9 show that the estimates of the basic treatment effect are quite robust when adding local economic control variables. For example, the decrease of the basic LEZ treatment effect that is observed between the specifications in column (4) and (5) equals a difference in reduction of 1.5 days per year. However , none of the economic controls are significant in that specification, meaning that the fixed effects already capture a lot of the regional variation over time. Even in column (3), where no fixed effects are used, the influence of the additional variables is extremely small and barely significant. Hence , it can be concluded that the exclusion of economic controls in the main analysis does not pose a threat to the validity of the estimates. For the advanced LEZ, it seems like there is a large change in the treatment effect between the original specification in table 4 and table 9. However , this can be attributed to the fact that in the sample 2004–2009, only one station was treated with an advanced LEZ, while it was 14 in the original sample. Moreover , with respect to evaluating the influence of local economic conditions, the results throughout the specification show this treatment effect is not sensitive to adding the control variables as well.
Table 9: Adding economic control variables [Table not shown]
In a second test, it is examined if the results are driven by the fact that some cities contribute several measuring stations to the data set, while others only are included with one station. This is especially relevant since it is mostly the large cities that are equipped with several stations. Recalling from section 7.2 that it was also the large cities for which a treatment effect was found, it will be tested if the exclusion of all but one station from each city from the sample changes the average treatment effects15. Stations were chosen according to the following rule: The station with the longest observation period per city was kept in the sample, if two stations were active in the same time period, the one with the higher average pre-treatment concentrations was chosen. In total, 32 stations were dropped, of which 18 were control stations and 14 treated stations. As can be seen from table 10, the results vary only to a very small extent in comparison to the results using the complete sample. The treatment effect for the basic LEZ on 24h limit violations indicates for example a reduction of 4.7 non-compliance days per year when keeping only one station per city, while it was 5.2 in the original model. The effects on the monthly average concentration also only change marginally. Thus , it can be concluded that the results are insensitive to the overrepresentation of some cities in the sample.
Table 10: Keeping only 1 station per city [Table not shown]
Footnotes
13 See for example Wooldridge (2002), chapter 11.2
14 [Footnote text not visible in original]
15 In a further robustness check, it was tested if it is actually the very large cities that drive the treatment effects. Thus, a model where all cities with over 1 million inhabitants were excluded was estimated. The average treatment effects proved to be insensitive and can be found in table A4 in the appendix.






