Abstract

When calculating the numerical solution to a partial differential equation, effciency in the use of computer resources is desired when creating a mesh. By adapting the mesh to have a higher resolution only in the areas where it is needed, instead of everywhere, both the memory and computational resources are used in a more efficient way. This paper examines some recent publications regarding the implementation of structured adaptive mesh refinement on parallel systems and where future research in this field might lead.

1 Introduction

When solving numerical problems, especially partial differential equations (PDEs), the standard approach is to create a discretization, a mesh, of the domain of calculations. It is then possible to apply some numerical method, for example a finite difference method (FDM) or a finite element method (FEM), to solve the differential equation at hand.

The accuracy and stability greatly depend on the mesh that is being used. In complex problems, the mesh might have to have a very fine resolution, meaning the step size in time or space must be very small. The simplest way to accomodate this is to use the same resolution over the whole domain, but this increases the memory demand and the computational complexity. If the mesh does not have to have as fine a resolution everywhere, this is a waste of resources.

One method to help resort this problem is called Adaptive Mesh Refinement (AMR), which enhances the resolution of the mesh only where needed. AMR is increasingly being used in the scientific community on a large scale [2]. In this paper, structured AMR (SAMR) is discussed, which is adaptive mesh refinement on a structured grid, for example a Cartesian grid.

SAMR is a choice method for effficient spatial discretization of multiscale computational problems [3]. Here, for each time step and for each region, an a priori estimate of the error is calculated. The regions with an error exceeding a certain threshold are then flagged for refinement. This is repeated recursively until sufficient accuracy is reached on the whole domain. Note that the spatial mesh may be different for different time steps.

It is of course important The infinitive marker toto be able[/annotax] to do the SAMR algorithm in an efficient way, so that the method provides stable results. When implementing it on a parallel system, there are further complications, such as load balancing, minimizing communication and synchronization overheads, and partitioning the underlying grid hierarchies at run-time to expose all inherent parallelism.

The main function of parallel computing is to distribute data and work load among processors. However , with SAMR, the workload constantly changes and we need some dynamic load balancing. Methods for this include, for example, the Recursive Coordinate Bisection method (RCB), further detailed in section 2.

The next section will focus on describing, explaining and discussing different implementations of SAMR, with respect to different applications, and how various problems may arise and be dealt with. This information has been drawn from five articles published within the past two years. The final section presents conclusions about the information and makes predictions about where future research might lead. Discussions of ethical and societal aspects of this research are included as an appendix.

2 Applications and implementations

The outline of this section is as follows: To start, (2.1) will detail some direct applications of SAMR, including the Navier-Stokes equations, the discrete Boltzmann equation and various applications in magnetohydrodynamics. In (2.2), related problems with SAMR in parallel settings, such as scaling the algorithm to a high number of cores and visualizing data generated with the help of SAMR, will be discussed.

2.1 Direct applications of SAMR

SAMR is employed in a wide range of applications, and a few are presented in this section. One of them consists of the Navier-Stokes equations, which model fluid dynamics. For incompressible fluids, they take on the form

(1)

with ∇ · (u) = 0. Here u is the velocity vector, p is the pressure, ρ is density, μ is dynamic viscosity, and g ≈ 9.81 represents gravitational accleration.

 

While great Using the passive voiceprogress has been made to solve the Navier-Stokes equations numerically, the authors of [1] point out that[/annotax] :

“…the required mesh resolution to accurately resolve small scale fluid motions…remains as a limitation”

The same general meaning is in the paper [5] about the discrete Boltzmann equation for nearly incompressible single-phase flows:

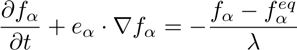 (2)

where f is the particle distribution function, t is time, λ is a relaxation parameter and e is the microscopic velocity.

Although SAMR may be used to combat this computational limitation, the workload will as a result vary greatly in a parallel system and Verbs and the -s endingneeds to be fixed using some load balancing algorithm[/annotax] . One of these is the Recursive coordinate bisection method (RCB), which is used in [1]. The authors there implement a parallel version to solve two problems, one involving the flow around a static object and one involving a sliding lid cavity.

The authors of [5], knowing that an AMR scheme has been tried before for the lattice Boltzmann method, point out that it was done with a quadtree structure. According to them, this is in itself inefficient for a parallel implementation involving many processing cores. The new approach uses a network of pointers to connect different grids in the mesh instead of a tree structure, which in turn makes it very easy to implement and execute in parallel. [5]

Not all problems are well suited for parallel SAMR. The authors of [5] show that cavity flow simulations (also performed in [1]) are not efficient for AMR because a substantial amount of computation is used for the AMR routine itself, while thin shear layer and vortex-shedding simulations show good speedup when using AMR.

Similarly , the author of [3] shows, through several simulations, that SAMR-based algorithms do not work well on certain types of problems related to hydrodynamics and magnetohydrodynamics. While it previously has been shown that SAMR is an efficient approach in these fields, and [3] reinforces this by showing efficient methods in two and three dimensions, the complexity of a curvilinear geometry prohibits certain types of experiments.

Calculations in hydrodynamics and magnetohydrodynamic have usually been performed on cartesian grids and less frequently on cylindrical or spherical grids. One reason for this is because construction and implementation of algorithms in these geometries becomes much more complex [3]. The new approach, developed in the paper, was included into NIRVANA, a parallel library built using MPI for various problems related to magnetohydrodynamics, which the author of [3] maintains and develops.

2.2 Problems related to implementation of SAMR

The various algorithms discussed in this paper, however theoretically fast, must also be implemented in an efficient way. This requirement is discussed in [2] in the framework of petascale and future exascale computers (with up to 100M cores). Exascale computers are expected to appear within the next decade [2] and it is of course important that numerical software using SAMR scale well in order to be useful on these future computers.

When talking about scaling, we distinguish between two terms:

Strong scaling : How the solution time varies with the number of processors for a fixed total problem size.

Weak scaling : How the solution time varies with the number of processors for a fixed problem size per processor.

In [2], different methods for refinement flagging and refinement creation are discussed in terms of how well they scale to larger systems. The authors perform numerical experiments for different algorithms related to SAMR for up to ≈ 99000 cores and use that to theoretically model strong and weak scaling for up to 100M cores. They emphasize that computing and communicating global metadata eventually starts to become a bottleneck and therefore that local algorithms are neccessary. This can be assumed to be true for the algorithms in [1, 3, 5] since this information is new and frameworks have not yet been updated to lessen their dependence on global metadata, according to the authors of [2]. Luckily, the same article also shows that grid creation for block-SAMR can be done without global metadata, in other words completely locally.

It is not always enough to just calculate solutions. When trying to visualize data generated for example by a PDE solver, the increased complexity of the mesh made by SAMR creates problems also for visualization. To understand this, the reader first needs to be familiar with the concept of raycasting.

The method of raycasting can be explained as follows: For each pixel on the screen, there is an imaginary ray from the eye of the observer into the virtual scene. Depending on what objects the ray encounters, the pixel it passed through will be coloured accordingly. Using standard visualization techniques like raycasting to datasets generated by SAMR is challenging because of less homogeneity in the structure of data.

The authors of [4] present ideas to perform this graphics rendering on a parallel system, more specifically a graphical processing unit (GPU) which itself is a parallel computational device. They present two different methods, a “packing” approach and a method based on NVIDIA’s Bindless Texture extension for OpenGL. These were applied to large datasets to see how the rendering can be done efficiently not just in time but also in terms of memory usage and band-width, which may be more limited on weaker systems. Results show that the latter approach is well suited for datasets larger than the available GPU memory. While SAMR Verbs and the -s endingaims to decrease the memory usage by refining the computational mesh only where needed, the resulting datasets from the methods of [1, 3, 5] may still be very large, thus strengthening the support for the Bindless Texture method.[/annotax]

The next section will draw some conclusions  on the material presented in this section, together with some predictions on future research in this field as made by the authors of the articles cited.

3 Conclusions  and future research

All five articles indicate at least partially positive results for using SAMR in parallel environments for different applications. Preliminary results point to stable behaviour and second order of convergence for velocities when solving the Navier-stokes equations for incompressible fluids [1].

The proposed SAMR method in [5], not using a tree-type data structure, is easier to code and is also easy to execute in parallel compared to previous methods. The finite difference method used in [5] retains second order accuracy in time and the authors hint they will compare accuracy in space, as well as efficiency compared to more conventional Lattice Boltzmann Methods, in a future paper.

For non-cartesian grids such as cylindrical and spherical grids , the SAMR framework works well in two and three dimensions [3], but details of the actual computation pose most of the problems, coupled with the non-rectangular geometry. The problems are according to the authors mainly due to the nonlocal character of the boundary conditions. Data generated by SAMR has also been shown to be possible to be rendered effectively on a parallel accelerator (such as a GPU) [4]. The packing approach outperforms the multi-pass algorithm and both methods enable straight-forward implementations of new techniques that can be executed completely on the GPU, which will increase performance as the number of shader cores increase, as it is projected to do [4].

Algorithms that utilize global metadata do not scale well in the strong or weak sense, as shown by [2]. That paper shows that block-SAMR (BSAMR) can be done completely locally. However , frameworks today still depend on global metadata. The authors of [2] push for further research that aims to lessen and remove this dependancy in various frameworks to make algorithms scale better, in preparation for future petascale and exascale machines. This will, in theory, benefit all SAMR applications (including the applications covered in [1, 3, 5]) on peta- and exascale machines appearing in the future.

References

[1] Rafael Sene de Lima, et al.et al.[2] Parallel block-structured adaptive mesh refinement for incompressible Navier-Stokes equations. 14th Brazilian Congress of Thermal Sciences and Engineering (2012).[/annotax]

[2] J. Luitjens, M. Berzins. Scalable parallel regridding algorithms for block-structured adaptive mesh refinement. Concurrency Computation: Pract. Exper. (2011): 23:1522-1537.

[3] Udo Ziegler. Block-structured adaptive mesh refinement on curvilinear-orthogonal grids. SIAM Journal of Scientific Computing vol. 34, no. 3 (2012): C102-C121.

[4] Ralf Kaehler, Tom Abel. Single-pass GPU-raycasting for structured adaptive mesh refinement data. SPIE Vol. 8654 865408-1 (2013).

[5] Abbas Fakhari, Taehun Lee. Finite-difference lattice Boltzmann method with a block-structured adaptive-mesh-refinement technique. Physical rreview E89, 033310 (2014).

4 Appendix: Ethics and societal aspects

It is rarely mentioned explicitly in scientific articles of computational science, but the researches performed usually have ethical aspects to them, both in how the research has been done but also how it is presented. Furthermore , research affects the society we all live in. Today, when our day-to-day life is filled with technology, this is perhaps more true than ever. This appendix will analyze some ethical and societal aspects of the articles discussed in this paper.

Every paper is authored by more than one author, except [3]. While the latter is not neccessarily bad or even uncommon in the scientific community, it is perhaps easier, Pairseither by intent or by external pressure, to influence[/annotax] the outcome of the research when only one person is responsible. Another notable exception regarding authors is the paper [4] where the authors originate from a well known high-ranking university (Stanford). This should of course not influence the reception of the article, but perhaps it does.

Only two, although different, applications are tested by the authors of [1], but they also conclude their results to merely be preliminary. For load balancing, they use the ZOLTAN library which is freely available. There are many authors to the article, which perhaps makes the likelihood of fraud less likely, as opposed to the single author in [3]. The main drawback to the paper is that we cannot easily recreate the results.

The reason for the difficulty of recreating results stems from something all five articles have in common: Nowhere is the actual code specified, and even the details of the computer system used vary. There is no mention of system details or implementation specifics at all besides the number of cores in [1]. Other papers are not as restrictive. Even so, with just the computer system used specified, and varying levels of detail in the mathematical deduction in [1, 3, 5], it is difficult to recreate the authors’ implementations exactly.

The hardware specified in [4], especially the graphics cards, are expensive but are supplied by the NVIDIA corporation. This probably leads them to have an interest in the actual results, but of course does not mean there is any actual influence. The reader should, however , keep this in mind seeing as how the result actually is positive for NVIDIA. Two different approaches are given in order to show which one is better. If the authors prefer one, this might influence which tests are run and presented and thus also influence the outcome and conclusions of the paper.

Just as for the other papers, there is no example code given in [4] to test the new GPU rendering algorithms for other datasets. Even the datasets used in the paper have not been made publically available. Perhaps one could contact the author or the original supplier of the data to get access, but this possibility is not mentioned.

The main point of [5] is that using a tree is an inefficient method. The authors show that their new method sometimes is useful, but not always, and thus put themselves in a very honest position presenting negative results. The timings of the numerical runs presented in Table IV [5] form the basis for the authors’ conclusion, but nowhere is it mentioned exactly how the timings are performed. This opens up questions: Is the current method ill-suited and would other timing methods yield worse results? Either way, the four different problems in the problems are diverse, but the authors themselves point out that their results are not universal because of the mixed results. The article itself is put into context and ideas for future research are mentioned.

The authors of [2] look at up to 98304 cores and use this to make a mathematical model to make predictions for scalability up to 100M cores. Being forced to use a theoretical model is understandable, since there is no 100M core computer available today (2014). However , since this value is three orders of magnitude higher than the actual runs, it begs the question of whether or not the model is accurate. This is reflected in the paper as the authors use words like “should” and not “will”. The research does not affect anything today but points to where future research should go – towards removing global metadata dependencies. The provided data is said to be a universal result for all algorithms, but drawn from analysing only the two in the paper.

Many numerical examples are run in [3] and the author points to future research by highlighting inefficiencies in his current approach. However , it is of course not known whether it is even possible to resolve the problem in this way. Maybe this method simply is inherently bad? Again, no code is provided, just the mathematical deduction. The reader only knows that the implementation uses MPI. References to many other code bases are done in the beginning which puts it into context and no one framework is “marketed”.

Nearly everything covered by the articles cited in this paper consists of gradual improvements upon already existing technology, ranging from the applications of SAMR to Navier-Stokes equations [1] to visualizing data generated by the solution of any PDE [4]. It is in practice impossible to determine how these technologies will be applied in the future, and it is therefore unfair to hold the scientists behind the articles [1, 3, 4, 5] accountable for future events caused by this, especially since they are merely a few of many advancing their respective fields. The only major influence tracable to a specific article occurs perhaps in [2] which asserts that global metadata is inherently bad and frameworks must be revised that perform SAMR more locally. This assertion is made on the basis of the authors’ mathematical model and may turn out to be false.

On the whole, the major deficiency of all the articles is the lack of code to actually reproduce the results, which seems to be not uncommon in this field.